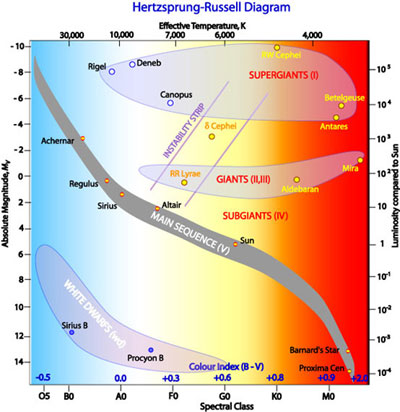
Lets take another look at the Hertzprung-Russell diagram. AKA as the color-magnitude diagram.

The diagram simply plots the temperature of a star vs its luminosity (presumably corrected for its dimming due to its distance). This simple graphic immediately reveals some startling groupings and relationships which are totally unexpected, and explaining these features has led to multiple questions which have led to some valuable insights in stellar evolution. Keep in mind that the H-R diagram is not a theoretical model, it is observational data. The patterns and spacings of dots on the diagram don’t tell you anything about stellar structure and evolution or stellar populations. But any answers you come up with to these questions must first explain what we see in the diagram, so it is a tool for understanding stars based on some of the very few things we can tell about them a priori. It is a constraint on our speculations. Google “Hertzprung-Russel” and select “Images” and you will find plenty of examples, many in color.

First, how do you correct a star’s brightness for its distance? All stars have an Absolute, or intrinsic, brightness (a property of the star itself) but they also have an Apparent brightness due to their distance from us (due to inverse square law). Since we have no way of knowing ahead of time how far away a star is from us, this presents a severe challenge. Astronomers got around this by first preparing H-R diagrams for star clusters, based on the perfectly reasonable assumption that just from its physical appearance, a crowded clump of stars floating in a sparse field, most of the stars will be neighbors to each other, and about the same distance from us. In other words, the distance between cluster stars is insignificant compared to the distance of the cluster from us. There may be a few non-cluster stars that either lie in front of the cluster or behind it, or that may just be coincidentally passing through it, but the vast bulk of them will have an apparent brightness directly related to their intrinsic brightness. An added bonus of this technique is that its also a reasonable assumption that all stars in the cluster formed at roughly the same time, from the same chemical mix of material and under similar conditions.

The brightness axis of the diagram is the y axis, the fainter ones are at the bottom, as you would expect, the brighter ones at the top. However, stars span an enormous range in brightness, the faintest are thousands of times fainter than the brightest, so to make them all fit on one graph the units of the y-axis are usually in apparent magnitude, unless we already happen to know how to correct for distance (as a rule, we don’t). Magnitudes are a power law, they are not evenly spaced. For example, each magnitude is approximately 2.512 times brighter than than the magnitude below it. This is an artifact of the way the human eye and photographic emulsions respond to light. We tend to perceive equal ratios of brightness as equal increments. The faintest stars we can see with the naked eye is about magnitude 6. A star 2.512 times brighter is magnitude 5, and so on. So the faintest star we can see is about a 100 times fainter than a first magnitude star. And of course, there is no reason a star can’t be brighter than that, so soon we are going past zero into negative numbers. The smaller the magnitude, the brighter the star. Mathematically defined, the log (base 10) of the light intensity ratio = 0.4 times the magnitude difference. So if two stars are one magnitude apart in brightness, the brighter is about two and a half times brighter than the fainter. (0.4 x 2.512 = 1). This may seem a cumbersome way to calculate brightness, but it allows us to easily compare enormous brightness differences in your head, with simple math. Also, since most methods for simultaneously determining the brightness of large numbers of stars (like measurements of images on photographic plates) are not particularly accurate, a precision of about a tenth of a magnitude is about the best we can hope for. It has the added advantage that the precision of the magnitude value is smaller for fainter stars, which is just what you would expect for this type of manual estimate: the brightness of extremely faint stars are more prone to uncertainty due to observational limitations.

So don’t be too startled if the numbers on the y-axis get smaller as you go up. It still means the brightness is increasing in that direction. Sometimes the y-axis units are in terms of Absolute solar brightness, in powers of 10. Again, this is done to be able to squeeze the enormous range of possible stellar brightness into a reasonably sized space on the page.

Both for historical reasons, as well as the response of film emulsion and the human eye to brightness, astronomers still prefer to speak in terms of magnitude instead of luminosity. It also
allows the rapid conversion to magnitude of a stellar image on a photographic plate–you just multiply the image size in microns by a constant to get the magnitude, and the constant is determined by how certain (predetermined) calibration stars appear through that telescope and that emulsion. There is a network of reference stars scattered throughout the sky that have been very accurately measured using other techniques, so if a few of them fall on your negative, you can immediately determine the magnitude correction for all the stars taken through that telescope with that film.

If you think the y-axis is confusing, now get a load of the x! The H-R diagram lists the temperature of the stars along the bottom, but the temperature DECREASES from left to right. just opposite of what you would expect from a graph. So the hottest stars are on the left, and the coolest on the right. Not only that, the temperature can be listed in several different ways. One is by simply listing the temperature in degrees Kelvin, from many tens of thousands of degrees for blue stars on the left, to several thousand degrees for red stars on the extreme right. Stars are black-body radiators, so the surface temperature is highly correlated with the color (Blue, White, Yellow, Orange, Red, going from L to R). Our yellow-white sun, by the way, is just under 6000 deg K. Sometimes the HR diagram is color coded, other times the x-axis is marked by spectral class (from hot to cold, left to right) O, B, A, F, G, K, M. The alphabet soup is a relic of when the spectral classes were first determined–before it was known how they related to temperature. The spectra used to assign spectral class were all observed with microscopes on black and white film, so the alphabet got scrambled up a bit after we knew which color/temp went with which class.

Great, but that still doesn’t explain why the H-R diagram x-axis DECREASES to the right. This too is an artifact of how stellar colors were measured en masse before color films were invented. Astronomers used two types of black and white film emulsions/filter combinations: B (Blue-sensitive) and V (Visual, or a film emulsion with roughly the same response to color as the human eye. Star images were dutifully measured by graduate students hunched over microscopes on both the B and V plates, and the magnitudes derived from the calibration stars I mentioned above, yielding both a Blue and a Visual magnitude for each star.

The hot stars would appear brighter (bigger) on the Blue plates and the cooler stars would appear brighter on the Visual plates, so simply subtracting the Visual from the Blue magnitude would give a number (called the B-V, or Color Index) which was highly correlated
with the star’s surface temperature. Using cheap grad student labor, this could be done for the thousands of stars that might appear on just two plates of the same star field. Today, I suspect the work is automated with CCDs, computers and scanners but the results are still represented this way so they can be compared directly with earlier work.

So for the hottest blue stars, type O, with temperatures close to 38000 deg K, the Color Index B-V would be about -0.32. The coolest red M stars with surface temperatures of about 2700 deg K have a Color Index of about +2.0. Our own G type sun has a surface temperature of 5900 and a B-V of +0.6. Class A stars (10800 deg) have a Color Index of 0.0. Note that since information comes from both photographic plates. we can tell a star’s temperature from its color, we don’t need to know its distance, the brightness of the star doesn’t matter, because its the difference in magnitudes which give the temperature estimate.

And THAT’S why the temperature scale on the H-R diagram decreases from L to R. The numerical value of the Color Index increases for cooler stars.

So what do we see on the H-R? White dwarfs in the lower left corner, white giants in the upper left. Red giants cluster in the upper right, and red dwarfs in the lower right. Certain unusual types are scattered here and there across the diagram, and the Main sequence slashes across it diagonally. We know now that as stars run out of thermonuclear fuel and evolve off the main sequence they appear to move to other parts of the graph, but a scarcity of stars in these intermediate spots tells us these shifts in position occur rather quickly (in astronomical terms). They simply don’t spend enough time in these transition zones that we’re likely to catch one there during our relatively brief lifetimes as humans. The few stars we do see in these “instability zones” are usually going through some severe internal readjustments, and manifest themselves by variability, conventional novae, planetary nebula stages or other outbursts of peculiar behavior. Some day, our own sun will pass through one or more of these episodes, probably freezing or incinerating any life that may still be on earth when it happens.

By compiling these graphs for many star clusters we can deduce their age, since the point at which stars evolve off the Main Sequence moves along the M-S line over time. The more massive, brighter, bluer stars evolve much faster. Older clusters have older stars evolving off the M_S line now, so we can think of this “evolving up” spot peeling up (to the R) of the M-S, and which tells us the age of the cluster.

The H-R diagram is stellar astronomy’s Periodic Table. It is a purely conceptual man-made tool which nevertheless gives us a powerful insight into the structure and evolution of stars.

I once worked with a woman who used to be one of Dr. Russel’s students. He always referred to it as the Russel-Hertzprung diagram.

http://astronomy.swin.edu.au/cms/cpg15x/albums/userpics/hrdiagram1.jpg